你被骗了！牛顿定律不是牛顿先发现的

天玑算

牛顿肖像画。图片来源：wikipedia

相信大家在中学课本上都学过牛顿运动三定律：惯性定律、加速度定律、作用力与反作用力定律。1687年，牛顿在《自然哲学的数学原理》中系统的提出了这三条定律。但其实，这三条定律并非完全由牛顿首创。

牛顿本人在《自然哲学的数学原理》中就曾提及，前两条定律的思想应归功于伽利略。而在牛顿之前，翰内斯·沃利斯（Johannes Wallisius）、克里斯托弗·雷恩（Christophorus Wrennus）和克里斯蒂安·惠更斯（Christianus Huygenius）就已先后提出过与牛顿第三定律类似的动力学原理。而牛顿的贡献则在于，从他们的研究成果中进行提炼与整合，最终总结出了更为简洁明了的牛顿第三定律。

正如牛顿在给自己的死对头——罗伯特·胡克（Robert Hooke）的回信中写到的一样：“如果说我看得比别人更远些，那是因为我站在巨人的肩膀上。”（If I have seen farther, it is by standing upon the shoulders of the giants）

不过最近越来越多解读认为，牛顿这样写并不是为了表达自己的谦卑，而是为了嘲讽胡克身材矮小。胡克年轻时就患有严重的驼背，他和牛顿还在科学观点上有诸多冲突。其中最广为人知的争议，莫过于关于万有引力定律的归属之争。胡克曾公开宣称，牛顿剽窃了他关于万有引力的研究思路。作为回应，当时在科学界权势极盛的 “牛爵爷”（牛顿）采取了强硬手段，导致胡克的所有画像都未能留存下来。如今，我们竟无从知晓这位在科学史上留下重要印记的伟大科学家 —— 胡克的真实样貌。

1680年绘制的一幅数学家画像，推测可能是胡克的画像，但也可能是其他人。图片来源：wikipedia

这两位科学巨匠的冲突也印证了一个事实：一条科学规律的最早发现者究竟是谁，结论往往充满争议且难以厘清。实际上，科学史上类似的例子不胜枚举 —— 有不少被冠以 “张三” 之名的定理，其最早发现者并非 “张三” 本人。

比如我们熟知的高斯分布（Gaussian distribution，即正态分布）最早并不是由高斯发现的。法国数学家亚伯拉罕·棣莫弗（Abraham de Moivre）早在1733年就引入了这种数学工具，而它则是在 1794 年，被冠以 “高斯” 之名。

在天文学领域，用于计算宇宙膨胀速度的哈勃定律，其雏形也并非由埃德温・哈勃（Edwin Hubble）最早提出。比利时物理学家乔治・勒梅特（Georges Lemaître）提出类似定律的时间，比哈勃还要早两年

再看密码学中广泛应用的RSA 加密算法，它以麻省理工学院的三位教授罗纳德・李维斯特（Ron Rivest）、阿迪・萨莫尔（Adi Shamir）和伦纳德・阿德曼（Leonard Adleman）的名字命名，三人于 1977 年共同发表了这一算法。但鲜为人知的是，英国数学家克利福德・柯克斯（Clifford Cocks）早在 1973 年就已在工作文件中提出了相同的算法，只是这一发现被英国政府通讯总部列为机密，直到 1997 年才得以公开。

施蒂格勒命名法则

在英文里，有一个专门的词汇eponymy（名祖命名法），用来指代这种以某人名字为定律、发明冠名的方式。但我们刚才已经看到了大量反例，如果继续探究下去，还有很多反例等着你发现。事实上，大部分定律、发明的冠名都或多或少存在与最初发现者不符的情况。而这一现象本身，甚至也成了一条规律 ——“施蒂格勒命名法则”（Stigler's law of eponymy）。

1980 年，美国芝加哥大学的统计学教授史蒂芬・史蒂格勒（Stephen Stigler）提出了这一法则，相关论文便以《施蒂格勒命名法则》为题。其最简洁的表述是：

“没有任何科学发现是以其最初的发现者命名的。”

历史上，许多发现的功劳往往归于将其发扬光大的人，而非最初的发现者；而且，同一时间段内多人独立得出相同新想法的情况也屡见不鲜，比如牛顿与莱布尼茨关于微积分发明权的著名争议，便是典型例证。

有趣的是，施蒂格勒命名法则自身也完美契合这一规律。史蒂格勒本人就将该规律的最早发现者归功于美国社会学家罗伯特・默顿（Robert Merton）—— 默顿早在 1968 年就注意到了类似的现象。更早之前，1903 年，著名作家马克・吐温（Mark Twain）在给海伦・凯勒的信中，也曾写下一段意涵相近的话：

“发明电报、蒸汽机、留声机、照片、电话或任何其他重要的东西，都需要上千人共同努力——而最后一人却获得了全部的功劳，我们则忘掉了其他人。他只是添了一小份力——这就是他所做的全部。这些例子应该教会我们，所有源于智慧的成果中有九成九都是纯粹的抄袭；这教训应该让我们谦逊。但没什么能做到这一点。”

严谨表述

然而，施蒂格勒命名法则的表述存在明显瑕疵，从逻辑层面看，只要能找出一个以最初发现者命名、“名副其实” 的定律，就能将其证伪。2022 年，美国数学家埃兹拉・布朗（Ezra Brown）和阿德里安・赖斯（Adrian Rice）在数学科普杂志《数学地平线》（Math Horizons，美国数学协会面向对数学感兴趣的大学生发行的刊物）上，发表了数学版本的施蒂格勒命名法则，对这一现象给出了更严谨的阐释。

他们提出：设n是数学中已经命名的定理、公式总数，p(n)是这些成果以最初发现人（们）命名的数量，那么：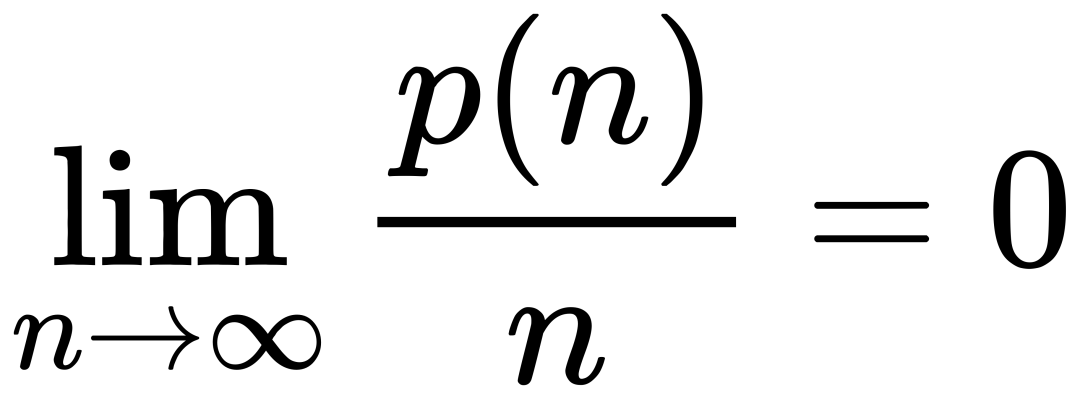

数学领域中以最初发现者正确命名的成果占比极低 。通俗来讲，数学规律里，能精准对应最初发现者的命名少之又少

文章作者还很幽默的把这个规律命名为布朗定律，布朗定律自身的也符合布朗定律——它最初不是由布朗提出的。布朗定律其实比施蒂格勒命名法则更弱。但反过来说，施蒂格勒命名法则很容易被偶尔的反例驳倒，布朗定律就不会受到这种影响。

符合施蒂格勒命名法则的例子还有很多。在维基百科上，从字母A-Z开头的定律，都有不少符合施蒂格勒命名法则的定律。例如，欧拉数e最早是由雅各布·伯努利（Jakob I. Bernoulli）注意到的；阿拉伯数字其实起源于印度；描述分布对数规律的本福特定律最早也是由天文学家西蒙·纽康发现的；就连快速傅里叶变换这个让大家能愉快刷短视频的算法，都经历了好几轮独立发现……

维基百科页面表示目前的列表还不完整，但已经足够填满从A到Z的目录了。

世界一直都是一个草台班子。说不定现在，还有理论深埋在厚厚的文献下，它们或许有改变世界的潜力，但是并不为人所知。只有当另一个人独立发现，或者剽窃原作者的创意，将它发扬光大，它才能发挥自己应有的作用。

你还知道哪些类似的“牛顿定律”？欢迎在评论区分享！

本文内容来源于中科院物理所，版权归原作者所有，如有侵权请联系删除，谢谢！